portafolioleyconservacionenergia


	portafolioleyconservacionenergia


	1.2.3 Potencia

1.2.3 Potencia

La potencia mecánica es la potencia transmitida mediante la acción de fuerzas físicas de contacto o elementos mecánicos asociados, como palancas, en granajes, etc.

El caso más simple es el de una partícula sobre la que actúa una fuerza constante o variable. De acuerdo con la mecánica clásica, el trabajo realizado sobre la partícula por dicha fuerza es igual a la variación de su energía cinética (energía de movimiento), por lo que la potencia desarrollada por la fuerza es:

$P=frac{dW}{dt} = frac{d}{dt}left( frac{1}{2}mv^2right) = frac{1}{2}frac{d}{dt}left(mmathbf{v}cdotmathbf{v}right) = frac{d}{dt}left(mmathbf{v}right)cdotmathbf{v} = mathbf{F}cdotmathbf{v}$

Alternativamente se puede calcular de la siguiente forma:

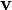$P=frac{dW}{dt} = frac{d left( F cdot x right)}{dt} = frac{d left( m cdot a cdot x right)}{dt} = m a frac{dx}{dt} = mathbf{F} cdot mathbf{v}$

Donde:

$mathbf{m}$ es la masa de la partícula.

$mathbf{F}$ es la fuerza resultante que actúa sobre la partícula.

$mathbf{v}$ es la velocidad de la partícula.

$mathbf{x}$ es la distancia de desplazamiento durante la que se ejerce la fuerza F.

En sistemas mecánicos más complejos con elementos rotativos alrededor de un eje fijo y donde el momento de inercia permanece constante, la potencia mecánica puede relacionarse con el par motor y la velocidad angular. De acuerdo con la mecánica clásica, el trabajo realizado sobre el cuerpo en rotación, es igual a la variación de su energía cinética de rotación, por lo que la potencia desarrollada por el par o momento de fuerza es:

$P=frac{dW_text{rot}}{dt} = frac{d}{dt}left(frac{1}{2}I_romega^2right)= M omega$

Donde:

I r

es el momento de inercia según su eje de giro.

ω

es la velocidad angular del eje.

M

es el par motor aplicado sobre dicho eje.

Si el movimiento rotativo tiene lugar alrededor de un eje variable la expresión correcta es:

$P= frac{dW_text{rot}}{dt} = frac{d}{dt}left(frac{1}{2}boldsymbolomega , mathbb{I} , boldsymbolomegaright) = frac{1}{2}left(boldsymbolomega cdot mathbf M + boldsymbolalpha cdot mathbf{L} right)$

Donde:

$mathbb I$ es la matriz o tensor de inercia.

$boldsymbolalpha$ es la aceleración angular del sistema.

$mathbf{L}$ es el momento angular del sistema.

$mathbf M$ es el momento dinámico actuante.

Esta última ecuación es análoga a la variación de potencia que se deriva de la ecuación del cohete donde al irse quemando combustible la masa no permanece constante.

En un flujo incompresible, la potencia mecánica asociada a la energía transmitida a las partículas del fluido, también puede expresarse en términos de presión y caudal:

$P= frac{dW_text{hyd}}{dt} = p Q$