1.1.6 Energia potencial y ley de la conservacion mecanica

Acabamos de ver cuando las fuerzas ejercidas sobre un cuerpo son conservativas, su energia cinetica podra disminuir durante su movimiento, pero a fin de cuentas sera recuperada al volver al punto de partida. Y si la energia cinetica es recuperable, cabe interpretar su disminucion suponiendo que transitoriamente ha queado "almacenada", o pasado a una forma potencial.



La energía potencial es energía que mide la capacidad que tiene dicho sistema para realizar un trabajo en función exclusivamente de su posición o configuración. Puede pensarse como la energía almacenada en el sistema, o como una medida del trabajo que un sistema puede entregar. Suele abreviarse con la letra 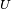o .

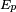La energía potencial puede presentarse como energía potencial gravitatoria, energía potencial electrostática, y energía potencial elástica.

Más rigurosamente, la energía potencial es una magnitud escalar asociada a un campo de fuerzas (o como en elasticidad un campo tensorial de tensiones). Cuando la energía potencial está asociada a un campo de fuerzas, la diferencia entre los valores del campo en dos puntos A y B es igual al trabajo realizado por la fuerza para cualquier recorrido entre B y A.

La energía potencial puede definirse solamente cuando la fuerza es conservativa. Si las fuerzas que actúan sobre un cuerpo son no conservativas, entonces no se puede definir la energía potencial, como se verá a continuación. Una fuerza es conservativa cuando se cumple alguna de las siguientes propiedades:

• El trabajo realizado por la fuerza entre dos puntos es independiente del camino recorrido.
• El trabajo realizado por la fuerza para cualquier camino cerrado es nulo.
• Cuando el rotacional de la fuerza es cero.

Se puede demostrar que todas las propiedades son equivalentes (es decir, que cualquiera de ellas implica la otra). En estas condiciones, la energía potencial se define como:

Si las fuerzas no son conservativas no existirá en general una manera unívoca de definir la anterior integral. De la propiedad anterior se sigue que si la energía potencial es conocida, se puede obtener la fuerza a partir del gradiente de U:

También puede recorrerse el camino inverso: suponer la existencia una función energía potencial y definir la fuerza correspondiente mediante la fórmula anterior. Se puede demostrar que toda fuerza así definida es conservativa.

La forma funcional de la energía potencial depende de la fuerza de que se trate; así, para el campo gravitatorio (o eléctrico), el resultado del producto de las masas (o cargas) por una constante dividido por la distancia entre las masas (cargas), por lo que va disminuyendo a medida que se incrementa dicha distancia.

La energía se conserva, es decir, ni se crea ni se destruye. Para sistemas abiertos formados por partículas que interactúan mediante fuerzas puramente mecánicas o campos conservativos la energía se mantiene constante con el tiempo:

.

Donde:

, es la energía cinética del sistema.

, es la energía potencial del sistema.

, es la energía potencial elástica del sistema.

Es importante notar que la energía mecánica así definida permanece constante si únicamente actúan fuerzas conservativas sobre las partículas. Sin embargo existen ejemplos de sistemas de partículas donde la energía mecánica no se conserva:

• Sistemas de partículas cargadas en movimiento. En ese caso los campos magnéticos no derivan de un potencial y la energía mecánica no se conserva, ya que parte de la energía mecánica "se convierte" en energía del campo electromagnético y viceversa.

quedar como energía interna o energía térmica de agitación de las moléculas o partes microscópicas del sistema.

• Sistemas termodinámicos que experimentan cambios de estado. En estos sistemas la energía mecánica puede transformarse en energía térmica o energía interna. Cuando hay producción de energía térmica, en general, existirá disipación y el sistema habrá experimentado un cambio reversible (aunque no en todos los casos). Por lo que en general estos sistemas aún pudiendo experimentar cambios reversibles sin disipación tampoco conservarán la energía mecánica debido a que la única variable conservada es la energía interna.